2019 - 2020学年上学期
高中二年级数学期中试题
说![]() 明:本试题分填空题和解答卷两部分,共160分,考试用时120分钟.
明:本试题分填空题和解答卷两部分,共160分,考试用时120分钟.
第Ⅰ卷(填空题 共70分)
1、填空题(本大题共14小题,每小题5分,共70分)
1.命题“![]() ,
,![]() ”的否定是____________________
”的否定是____________________![]() __________________________________________________.
__________________________________________________.
2.函数![]() 在点
在点![]() 处切线的斜率为______________________________
处切线的斜率为______________________________![]() __________.
__________.
3.若双曲线![]() 的焦距为
的焦距为![]() ,则其离心率
,则其离心率![]() __________________________________________________.
__________________________________________________.
4.函数![]() 的单调减区间为__________________________________________________.
的单调减区间为__________________________________________________.
5. 已知圆![]() 的圆心为抛物线
的圆心为抛物线![]() 的焦点,且与直线
的焦点,且与直线![]() 相切,则该圆的方程为______________________________________________________________________.
相切,则该圆的方程为______________________________________________________________________.
6. “![]() ”是“
”是“![]() ”成立的___________________________________________________条件.(从“充要”、“充分不必
”成立的___________________________________________________条件.(从“充要”、“充分不必![]() 要”、“必要不充分”中选择一个正确的填写)
要”、“必要不充分”中选择一个正确的填写)
7.抛物线![]() 上的点
上的点![]() 到焦点
到焦点![]() 的距离为5,
的距离为5,![]() 为坐标原点,则
为坐标原点,则![]() ______________________________
______________________________![]() __________.
__________.
8. 已知抛物线![]() 的准线经过双曲线
的准线经过双曲线![]() 的右顶点,则双曲线的渐近线方程为______________________________
的右顶点,则双曲线的渐近线方程为______________________________![]() __________.
__________.
9.已知圆![]() 过点
过点![]() ,且圆心在
,且圆心在![]() 轴的正半轴上.直线
轴的正半轴上.直线![]() 被圆
被圆![]() 所截得的弦长为
所截得的弦长为![]() ,则过圆心且与直线
,则过圆心且与直线![]() 垂直的直线的方程为______________________________.
垂直的直线的方程为______________________________.
10. 若函数![]() 在区间
在区间![]() 上有极小值,则实数
上有极小值,则实数![]() 的取值范围为__________.
的取值范围为__________.
11.已知F1,F2分别是椭圆![]() +
+![]() =1(a>b>0)的左右焦点,点A是椭圆的右顶点,O为坐标原点,若椭圆上的一点M满足MF1⊥MF2,|MA|=|MO|,则椭圆的离心率为____________________________________.
=1(a>b>0)的左右焦点,点A是椭圆的右顶点,O为坐标原点,若椭圆上的一点M满足MF1⊥MF2,|MA|=|MO|,则椭圆的离心率为____________________________________.
12. 已知直线![]() ,分别与直线
,分别与直线![]() 和曲线
和曲线![]() 交于点M,N两点,则线段MN长度的最小值是__________________________________________________
交于点M,N两点,则线段MN长度的最小值是__________________________________________________![]() __________.
__________.
13.在平面直角坐标系![]() 中,点Q为圆
中,点Q为圆![]() 上的一动点,直线
上的一动点,直线![]() 与直线
与直线![]() 相交于点P,则当实数k变化时,线段PQ长的最小值是__________________________________________________
相交于点P,则当实数k变化时,线段PQ长的最小值是__________________________________________________![]() __________.
__________.
14.已知函数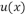 ,(
,(![]() 为自然对数的底数),若
为自然对数的底数),若![]() 使得函数
使得函数![]() 有三个零点,则m的取值范围是__________.
有三个零点,则m的取值范围是__________.
第Ⅱ卷(解答卷 共90分)
2、解答卷(本大题共6小题,共90分. 解答时应写出文字说明、证明过程或演算步骤)
15.(本题满分14分)
已知直线![]() .
.
(1)求过点![]() 且与直线
且与直线![]() 平行的直线方程;
平行的直线方程;
(2)若直线![]() 与两坐标轴所围成的三角形的面积大于4,求实数
与两坐标轴所围成的三角形的面积大于4,求实数![]() 的取值范围.
的取值范围.
16.(本题满分14分)
已知命题![]() :方程
:方程![]() 表示圆;命题
表示圆;命题![]() :方程
:方程![]() 表示焦点在
表示焦点在![]() 轴上的椭圆.
轴上的椭圆.
(1)若命题![]() 为真命题时,求实数
为真命题时,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
[来源:Z_xx_k.Com]
17.(本题满分14分)
已知圆![]() 一动直线
一动直线![]() 过
过![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点,![]() 是
是![]() 的中点,
的中点,![]() 与直线
与直线![]() 相交于
相交于![]()
(1)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)探索![]() 是不是与直线
是不是与直线![]() 的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
18.(本题满分16分)
一个创业年轻人租用一块边长为4百米的等边△ABC田地(如图)养蜂、产蜜与售蜜.田地内拟修建笔直小路MN,AP,其中M,N分别为AC,BC的中点,点P在BC上.规划在小路MN与AP的交点O(O与M、N不重合)处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物成长区,A,N为出入口(小路的宽度不计).为节省资金,小路MO段与OP段建便道,供蜂源植物培育之用,成本忽视不计.为![]() 汽车安全出入,小路AO段的建造成本为每百米4万元,小路ON段的建造成本为每百米3万元.
汽车安全出入,小路AO段的建造成本为每百米4万元,小路ON段的建造成本为每百米3万元.
(1)若拟修的小路AO段长为![]() 百米,求小路ON段的建造成本;
百米,求小路ON段的建造成本;
(2)设∠BAP=![]() ,求cosplay
,求cosplay![]() 的值,使得小路AO段与ON段的建造总成本最小.
的值,使得小路AO段与ON段的建造总成本最小.

19.(本题满分16分)
如图,椭圆![]() 的离心率为
的离心率为![]() ,焦点到相应准线的距离为1,点
,焦点到相应准线的距离为1,点![]() ,
,![]() ,
,![]() 分别为椭圆的左顶点、右顶点和上顶点,过点
分别为椭圆的左顶点、右顶点和上顶点,过点![]() 的直线
的直线![]() 交椭圆于点
交椭圆于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求椭圆的规范方程;
(2)若![]() ,求直线
,求直线![]() 的方程;
的方程;
 (3)求证:
(3)求证:![]() 为定值.
为定值.
20.(本题满分16分)
已知函数![]()
![]() .
.
求过点![]() 的
的![]() 的切线方程;
的切线方程;
当![]() 时,求函数
时,求函数![]() 在
在![]()
![]() 上的最大值;
上的最大值;
证明:当![]()
![]() 时,不等式
时,不等式![]()
![]() 对任意
对任意![]()
![]() 均成立.
均成立.
2019 - 2020学年上学期
高中二年级数学期中试题 参考答案
1、填空题(本大题共14小题,每小题5分,共70分)
1. ![]() ,
,![]() .2.
.2. ![]() 3.
3.![]() ,4.
,4. ![]() 如写成
如写成![]() 也正确
也正确
5. ![]() 6.必要不充分 7.
6.必要不充分 7. ![]() 8.
8. ![]()
9. ![]() 10.
10. ![]() 11.
11. ![]() 12.
12.![]() 13.2 ,14.
13.2 ,14.![]()
15.解:(1)与直线![]() 平行的直线的斜率为
平行的直线的斜率为![]() , ……………………2 分
, ……………………2 分
由于点![]() 在该直线上,
在该直线上,
所以所求直线方程为![]() , ……………………4 分
, ……………………4 分
即直线方程为![]() . ……………………6 分
. ……………………6 分
(2)直线![]() 与两坐标轴的交点分
与两坐标轴的交点分![]() 别为
别为![]() ,… …8分
,… …8分
则所围成的三角形的面积为![]() , …………10 分
, …………10 分
由题意可知![]() ,
,
化简得![]() ,
,
解得![]() 或
或![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() . …
. …![]() …………………14 分
…………………14 分
16.解:
(1)若命题![]() 为
为![]() 真命题时,
真命题时,
则由方程![]()
即![]() 表示圆, ……………………2 分
表示圆, ……………………2 分
∴![]() 解之得 ……………………4 分
解之得 ……………………4 分
∴![]() ……………………6 分
……………………6 分
(2)由![]() 成立得
成立得![]() ……………………8 分
……………………8 分
∴![]() ,
,
若![]() 是
是![]() 的必要不充分条件,则
的必要不充分条件,则![]() , ……………………10 分
, ……………………10 分
∴![]() ……………………12 分
……………………12 分
解之得![]()
∴![]()
![]() ……………………14 分
……………………14 分
17.解:(1)①当直线![]() 与
与![]() 轴垂直时,易知
轴垂直时,易知![]() 符合题意……… 1分
符合题意……… 1分
②当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]()
![]()
![]()
则由![]() ,得
,得![]()
![]() ……… 4分[来源:学§科§网Z§X§X§K]
……… 4分[来源:学§科§网Z§X§X§K]
……………………5 分![]()
综上,所求的直线![]() 的
的![]() 方程为
方程为![]() ………6分
………6分
![]()
![]()
当直线![]() 与
与![]() 轴垂直时,易得
轴垂直时,易得![]() ,
,
则![]()
![]() ……… 8分
……… 8分
②当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]()
则由![]() ,得
,得![]() , ……………………12 分
, ……………………12 分
则![]()
![]()
综上,![]() 与直线
与直线![]()
![]() 的斜率无关,因此与倾斜角也无关,
的斜率无关,因此与倾斜角也无关,
且![]() ………14分
………14分
18.解(1)在△AOM中,![]()
∴![]() …………………2 分
…………………2 分
化简得:![]()
∵![]() >0,∴
>0,∴![]() =1,
=1, ![]() …………………4 分
…………………4 分
则![]() ,3×1=3
,3×1=3
答:小路ON段的建造成本为3万元. ……………………6 分
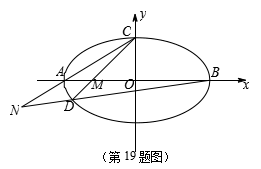
(2)由正弦定理得: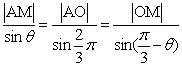
则![]() ,
,![]()
![]()
……………………9 分
设小路AO段与ON段的建造总成本为![]()
则![]() ,
,![]() ……………………11 分
……………………11 分
![]() ,若
,若![]() 满足
满足![]() ,且
,且![]() ,
,
列表如下:
|
| ||
| ﹣ | 0 | ﹢[来源:Zxxk.Com] |
|
|
|
|
则当![]() =
=![]() 时,
时,![]() 有极小值,此时也是
有极小值,此时也是![]() 的最小值
的最小值
∴![]() ……………………15 分
……………………15 分
答:当cosplay![]()
![]() ,小路AO段与ON段的建造总成本最小.……16 分
,小路AO段与ON段的建造总成本最小.……16 分

19.解(1)由椭圆的离心率为![]() ,焦点到对应准线的距离为1.
,焦点到对应准线的距离为1.
得 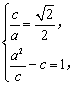 解得
解得![]() ……………………2 分
……………………2 分
所以,椭圆的规范方程为![]() . …………………4分
. …………………4分
(2)由(1)知![]() ,设
,设![]() ,
,
由于![]() ,得
,得![]() ,所以
,所以![]() , ………………6 分
, ………………6 分
代入椭圆方程得![]() 或
或![]() ,所以
,所以![]() 或
或![]() ,
,
所以![]() 的方程为:
的方程为:![]() 或
或![]() . ……………9 分
. ……………9 分
(3)设D坐标为可得直线![]() 的方程
的方程![]() ,
,
联立椭圆方程得: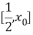 解得
解得![]() ,
,![]() . ……12 分
. ……12 分
由![]()
![]() ,得直线BD的方程:
,得直线BD的方程:![]() , ①
, ①
直线AC方程为![]() , ②
, ②
联立①②得![]() , ………………………………15 分
, ………………………………15 分
从而![]() =2为定值. ……………………………16 分
=2为定值. ……………………………16 分
解法2:设D坐标为设切点坐标为![]() ,则切线方程为
,则切线方程为![]() ,
,
将![]() 代入上式,得
代入上式,得![]() ,
,
∴切线方程为![]() ; ……………………3 分
; ……………………3 分
当![]() 时,
时,![]() ,
,
∴![]() , ……………………4 分
, ……………………4 分
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 递增,在
递增,在![]() 递减, ……………………6 分
递减, ……………………6 分
∴当![]() 时,
时,![]() 的最大值为
的最大值为![]() ;
;
当![]()
![]() 时,
时,![]() 的最
的最![]() 大值为
大值为![]() ; ……………………8 分
; ……………………8 分
![]() 可化为
可化为![]() ,[来源:学#科#网]
,[来源:学#科#网]
设![]()
,要证![]() 时
时![]() 对任意
对任意![]() 均成立,
均成立,
只须证![]() ,下证此结论成立. ……………………9 分
,下证此结论成立. ……………………9 分
∵![]() ,∴当
,∴当![]() 时,
时,![]() ,
,
设![]() ,则
,则![]() ,∴
,∴![]() 在
在![]() 递增, …11 分
递增, …11 分
又∵![]() 在区间
在区间![]() 上的图象是一条不间断的曲线,且
上的图象是一条不间断的曲线,且![]() ,
,
∴![]() 使得
使得![]() ,即
,即![]() , ……13 分
, ……13 分
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
∴函数![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,
∴![]() ,
,
∵![]() 在
在![]() 递增,∴
递增,∴![]() ,
,
即![]() ,
,
∴当![]() 时,不等式
时,不等式![]() 对任意
对任意![]() 均成立.
均成立.
……………………16 分







